Description

This study presents and evaluates two variational data assimilation techniques for the estimation of low order surrogate experimental dynamical models for fluid flows. Both methods are built from optimal control recipes and rely on proper orthogonal decomposition and a Galerkin projection of the Navier Stokes equation. The techniques proposed differ in the control variables they involve. The first one introduces a weak dynamical model defined only up to an additional uncertainty time-dependent function whereas the second one, handles a strong dynamical constraint in which the dynamical system's coeffcients constitute the control variables. Both choices correspond to different approximations of the relation between the reduced basis on which is expressed the motion field and the basis components that have been neglected in the reduced order model construction.The strong constraint assimilation allows us estimating the constant, linear and quadratic coefficients associated to the reduced flow dynamics together with its initial condition whereas the weak constraint assimilation enables to adapt further the initial condition and to recover the value of an additional uncertainty function associated to the dynamics.

The techniques have been assessed on numerical data and in real experimental conditions with noisy Image Velocimetry data.

Results

The assimilation techniques have been evaluated on a wake flow behind a cylinder at Reynolds 3900. An empiral POD basis has been built from experimental measurements provided through a PIV techniques. A snapshot of a typical vorticity map of such measurements is shown below.

The table below plots the trajectories of the 32 first temporal POD modes of the reduced dynamical system. A time range corresponding to three vortex sheddings (128 snapshots) is shown here. The dashed lines correspond to the observed temporal POD coefficients (every 2 snapshots instants) the solid lines depict the results of the strong constraint assimilation.

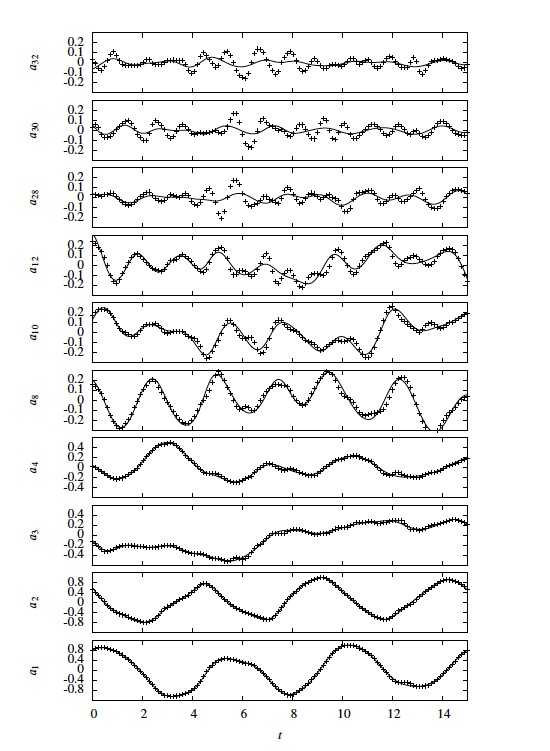
The following table shows with the same conventions as above the results of the weak constraint assimilation process.

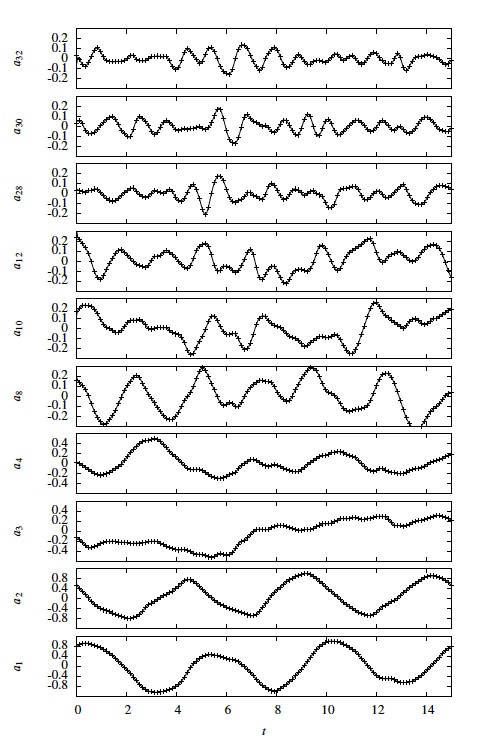
The initial condition and the uncertainty function provided by this second assimilation process allow the dynamical system to perfectly fits the data. The strong constraint assimilation process improves significantly the results of traditional low order dynamics identification techniques, which exhibit often stability problems as they do not supply an initial condition adapted to the reduced system's dynamics. This is particularly problematic when the experimental data includes important noise or inaccurate velocity measurements. The weak constraint assimilation process improves further the results by refining the construction of an adapted initial condition and supplies the estimation of an additive uncertainty variable attached to the dynamics. Such uncertainty variable can be interpreted as a time varying term of the dynamics representing both the coupling between the neglected secondary modes and the components of the POD basis. It incorporates also the eventual contribution of the projection of the fluctuating pressure gradient component on the POD temporal modes

References

G. Artana , A. Cammilleria , J. Carlier , E. Mémin, Strong and weak constraint variational assimilations for reduced order fluid flow modeling, J. of Computational Physics, conditionally accepted under minor revisions condition, 2011.