POD-Spectral Decomposition for Fluid Flow Analysis and Model Reduction

A. Cammilleri, F. Gueniat , J. Carlier, L. Pastur, E. Memin,  F. Lusseyran,  G. Artana

 
 

We propose an algorithm that combines Proper Orthogonal Decomposition with spectral method to analyze and extract reduced order models of flows from time data series of velocity fields. This methodology is specifically adapted to  flows driven by non linear dynamical systems exhibiting a complex behavior within a quasi periodic orbits in the phase space. The technique enables an easy model reduction specially in cases for which the underlying dynamics requires a discretization with a high spatial and temporal resolution. The proposed analysis enables to decompose the  flow dynamics into modes that oscillate at a single frequency. For each modes an energy content and a spatial structure can be put in correspondence. This approach is illustrated using data obtained from time resolved PIV of a cylinder wake  flow at Reynolds number 3900.

 

abstract

Brief method description

Legend

Upper frame: Vorticity maps derived from time resolved Particle Image Velocimetry velocity fields.

 

Bottom left frame: Reconstruction based on a spectral analysis of the temporal coefficients of a Karhunen Loeve decomposition of the PIV velocity field data. (number of modes considered 3070)


Bottom right frame: Identical reconstruction with a reduced model. Truncation criteria is based on the analysis of the energy spectra.  A cutoff of high frequencies modes is proposed considering the characteristics of Eulerian  time spectrum of turbulent flows.  (number of modes retained 1284)

Reconstruction results


where A denotes the vector gathering the POD temporal coefficient and V are the Koopman modes.  Each mode is associated to a single frequency and can be in practice obtained with a traditional spectral decomposition technique based on the companion matrix. Those modes can be associated to a spatial structure through the  summation of the POD spatial modes weighted by the Koopman modes amplitude. Keeping the eigenvalues that lie numerically within the unitary circle the last right hand equation above provides a way to predict future values of the POD temporal coefficients. Associated to a truncation procedure  (constructed in this work from a normalization related to the global fluctuating kinetic energy) this equation enables to select the most significant Koopman modes and to reconstruct  the data from a reduced basis. 



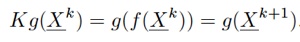
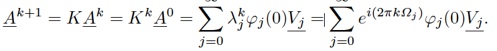
The method relies on a spectral decomposition defned through the use of the Koopman operator applied on a discrete dy-namical system

The Koopman operator (or compositional operator) is a linear operator associated to function f that relates  an observable function g of the system state variables X as

As a result the dynamical system can be analyzed through  the eigenvalues and eigenvectors of the Koopman operator

The eigenfunctions provide an orthonormal expansion basis. Associated  to Karunen Loeve decomposition of PIV velocity fields and successive application of the Koopman operator provide

The method has been assessed for a wake flow behind a circular cylinder at Reynolds 3900. We show below a movie depicting  some reconstruction results for this flow.

Reference